The free vibration characteristic of spherical cap with general edge constraints is studied by means of a unified method. The energy method and Kirchhoff hypothesis are adopted to derive the formulas. The displacement function component along axial direction is still the Fourier series. In addition, the spring stiffness method forms a unified format to deal with various complex boundary conditions and the continuity conditions at two adjacent segments.
Volume Of A Spherical Cap Derivation Then, the final solutions can be obtained based on the Ritz method. To prove the validity of this method, the results of the same condition are compared with FEM, published literatures, and experiment. The results show that the present method has the advantages of fast convergence, high solution accuracy, simple boundary simulation, etc.
In addition, some numerical results of uniform and stepped spherical caps with various geometric parameters and edge conditions are reported. Meanwhile, many related investigations have been conducted on typical curved shells and structures, such as the GDQ method, Fourier–Ritz method, radial basis function method, and so on. Jouneghani et al. investigated vibrational behavior of doubly curved shells on the basis of first-order shear deformation theory considering porosities. Hamilton's principle and Navier's solution method were both utilized to derive the numerical results. Wang et al. [7–9] analyzed vibration behavior of cylindrical shells on Pasternak foundation by means of Fourier–Ritz approach.
Jin et al. [10–12] analyzed vibration behavior of cylindrical shells with general boundary restraints by means of a generalized solution. The vibration behavior of a thin cylindrical shell with simply supported edges was studied by Wu et al. by means of Hamilton's principle. Lagrange principle and Hamilton's principle were utilized by Hussain et al. to investigate vibration of cylindrical shell resting on Winkler and Pasternak elastic foundations. Zhou et al. analyzed the free vibration features of cylindrical shells with elastic edge conditions. The method of wave propagations was utilized on the basis of Flügge thin shell theory. The author presented the displacement function by Chebyshev polynomials and Fourier series.
Tornabene et al. presented the radial basis function method to study vibration behavior of composite curved cases. Brischetto et al. introduced the zig-zag function to overcome the discontinuity of displacement function; free vibration of curved plates was analyzed. Lee et al. applied Flügge's thin shell theory and Rayleigh's energy method to analyze the free vibration characteristics of the joined spherical-cylindrical shell with general edge constraints. In addition, a modal test was conducted to validate the dependability of the method.
Shi et al. analyzed vibration behavior of double-curved shallow shells with complex edges on the basis of the spectral-geometric Ritz method. The displacement component was expressed as the assembly of Fourier series and assistant functions. The reliability and exactness of the method was proved through the comparison between present method, FEM, and published literatures. Wang et al. also proposed a unified formulation to investigate vibration behavior of curved shells. As we can see from the literature review, most studies mentioned above are restricted to classical edge constraints, such as clamped, hinged, and free boundary. To the authors' knowledge, few research studies have been conducted to study the vibration characteristics of uniform and stepped spherical caps with elastic edge conditions.
Therefore, a unified method is necessary and meaningful to establish to solve the vibration behavior of uniform and stepped spherical caps with elastic edge conditions. On the basis of theory of thin shell and the domain decomposition method, spherical caps are separated into sections along the meridian direction. The displacement components of spherical caps along meridian and circumferential directions are presented by Jacobi polynomials and Fourier series. The boundary restraints and the internal interfaces between two adjacent parts of spherical cap are simulated through the penalty method.
Final solutions are derived on the basis of the Rayleigh–Ritz method. The nondimensional frequency parameters of the current method with different segments are compared with the results of FEM and related literature in Table 2. H/Rc and of spherical cap are, respectively, 0.005 and 60 degrees. The elastic support edge constraints are imitated by distributed springs which are made up by 160 COMBIN 14 elements.
In addition, the spherical cap is composed of four-node element shell 63. There are 120 and 180 shell elements along meridian and circumferential directions, respectively. The mesh of the spherical cap is fine enough to guarantee the accuracy. It can be concluded from Table 2 that the current method converges well when the shell segment is small. When the shell segment reaches 4, convergence and exactness are completely fulfilled.
As seen in the table, a many number of shell segments are not required in this study. The subsequent calculations will be conducted when the shell segment is set as 4. Meanwhile, structures with stepped thickness exist widely in engineering application.
The dynamic features of this kind of structure also attract researcher's attention. Qu et al. put forward the domain decomposition method to investigate vibration behavior of stepped and homogeneous conical shells with various boundary restraints. Zhang and Xiang studied the vibration behavior of cylindrical shells with stepped thickness by means of the state-space technique and domain decomposition method. The influence of shell thickness ratios, locations of stepwise thickness variations, and step thickness ratios were also discussed.
Fazzolari carried out an investigation of vibration characteristic of curved shells on the basis of the dynamic stiffness method and higher order shear deformation theory. Xie et al. combined Flügge's thin shell theory with the power series method to investigate vibration characteristic of stepped curved shells with different edge conditions. Gautham and Ganesan conducted a research to deal with the free vibration characteristics of isotropic and laminated orthotropic spherical caps. Based on the first-order shear deformation theory, a semianalytical shell finite element was utilized to investigate the effect of geometric configurations on vibration behavior of spherical caps. Singh and Mirza studied the vibration characteristics of spherical shells with various boundary restraints by means of FEM. Natural frequencies of spherical shells with different geometry parameters have been analyzed.
Then, the author presented displacement fields of each segment by quintic Bezier functions, which was proved efficient and accurate using only two to four shell segments of spherical shells. Wu and Heyliger analyzed the free vibration of spherical caps on the basis of two-dimensional first-order shear deformable shell theory. Hermite interpolation polynomials and Fourier series were used in the azimuthal and circumferential direction, respectively. Figure 8 shows nondimensional frequency parameters Ω of uniform spherical cap with different center angles and boundary restraints .
It is easy to find that with the increase of center angle, the frequency parameter of spherical cap decreases, especially when the center angle is smaller than 50 degrees. In addition, the tiny distinction between the current method, related literature, and FEM proves high accuracy of the current method. Altogether, the current method works well when handling vibration analysis of uniform and stepped spherical cap with general boundary conditions by means of a generalized solution. That is to say, stiffness values at this stage can ensure clamped boundary restraints. Meanwhile, when the stiffness values of boundary spring are less than 104, the boundary conditions can be seen as free. When the spring stiffness values are in the range of 105 to 109, the boundary conditions can be regarded as elastic.
In the current research, the spring stiffness matching with free and clamped boundary restraints is, respectively, set as 0 and 1014. The spring coefficient kb of elastic support is set as 108 in the current research unless otherwise stated. Thus, the spring stiffness values of the general edge conditions can be achieved as shown in Table 1. In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane.
If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere. Figure 10 displays the relation between nondimensional frequency parameters Ω and stiffness of different elastic supports. In the previous clamped boundary restraint example, we soften the axial, radial, circumferential, and rotational spring stiffness continuously from 1014 to 100, respectively. The nondimensional frequencies Ω of the first circumferential mode and the first three meridian wavenumbers are considered. The similar trend in Figure 4 is discovered again when considering axial and circumferential elastic supports, respectively. However, the changes of stiffness value of radial and rotational spring have little effect on the frequency parameters Ω.
Frequency parameters Ω of stepped hemispherical cap with different boundary conditions using the current method and FEM. Nondimensional frequency parameter of stepped hemispherical cap with different edge conditions. The spherical cap is no different but a part of the sphere itself that falls over the plane of a sphere. If you know the values of the base area, radius, and the height of a sphere then this is easy to calculate the area of the shape. The other popular name for the spherical cap is spherical dome.
Sometimes, you will be given the base radius and sometimes you will be given the value of sphere radius. Frequency parameters Ω of uniform spherical cap with different center angles and boundary conditions. Comparison of frequency parameters of uniform hemispherical cap subjected to different edge conditions.
Nondimensional frequency parameter of uniform hemispherical cap with different edge conditions. Nondimensional frequency Ω of uniform spherical cap with various elastic support edge conditions. Typical mode shapes of the spherical cap with free edge conditions using different methods. Typical model test mode shapes of the spherical cap with free boundary restraint.
Typical mode shapes of the spherical cap with free boundary restraint using FEM software. Typical mode shapes of the spherical cap with free boundary restraint using the current method. The effect of boundary spring stiffness on frequency parameter of spherical cap varies greatly in different directions. Nondimensional frequency parameter of uniform 30 degrees spherical cap with different edge conditions.
Nondimensional frequency parameter of uniform 45 degrees spherical cap with different edge conditions. Nondimensional frequency parameter of uniform 60 degrees spherical cap with different edge conditions. H and hi, respectively, denote the thickness of uniform and stepped spherical cap. The symbols R, Rc, Cs, and denote the horizontal radius, radius, the center, and center angle of spherical cap, respectively.
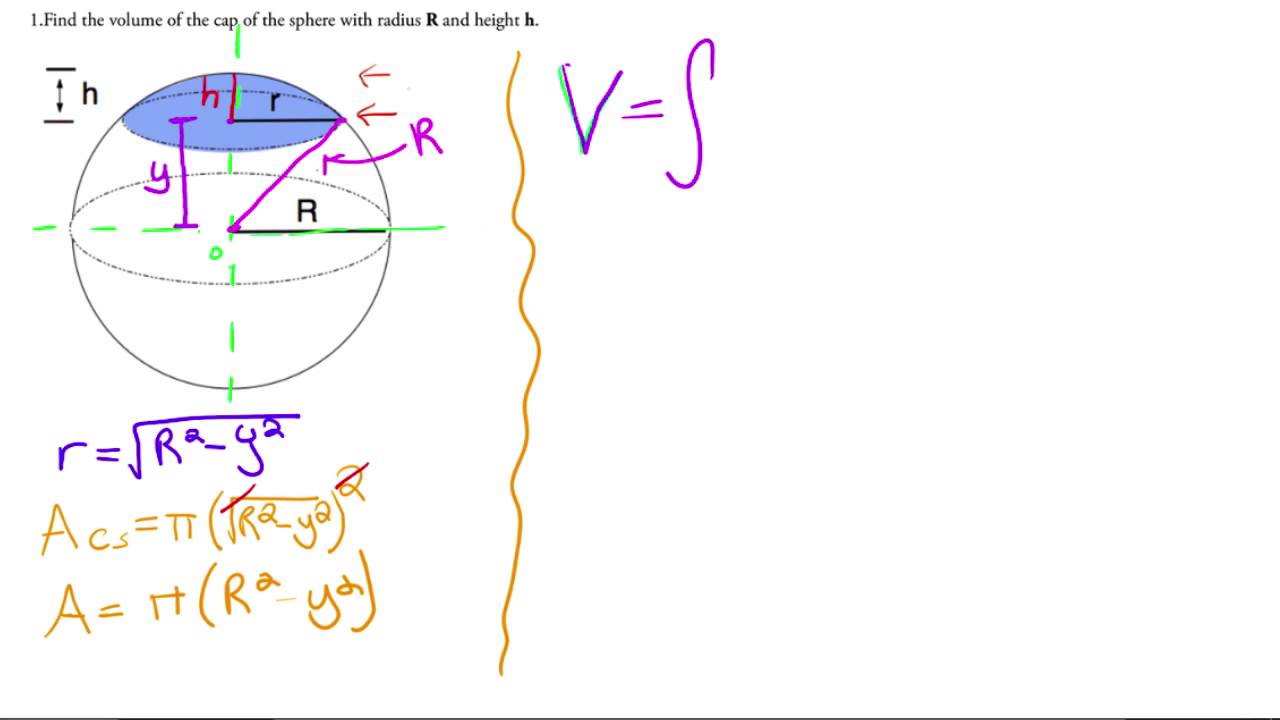
Figure 2 shows the differential element of the shell. This first result for a google search for "volume of sphere proof without calculus" should work for spherical caps as well. The spherical cap is the portion of a sphere that lies above a plane of the sphere. If the base area, height and the sphere radius is known then the volume can be found out of the particular portion. Spherical dome is the term used synonymously to the spherical cap. A spherical cap is the region of a sphere which lies above a given plane.
If the planepasses through the center of the sphere, the cap is a called a hemisphere, and if the cap is cut by a second plane, the spherical frustum is called a spherical segment. However, Harris and Stocker use the term "spherical segment" as a synonym for what is here called a spherical cap and "zone" for spherical segment. There is almost no effect of varying the radial and rotational restraining springs on the frequency parameters, while the other restraining stiffness is kept infinite. However, different trends appear when considering axial and circumferential elastic supports. To further verify the accuracy of the current method, the experiment test focusing on free vibration of a hemispherical cap was carried out. It should be pointed out that the spherical cap is isotropic.
In the current research, the continuity and the boundary restraints of spherical caps are simulated on the basis of the penalty method. Spherical caps have been widely used in many practical engineering branches, such as pressure vessels, dome-shaped structures, submarines, and nuclear power plants. These structures usually bear different extreme loads caused by wave, wind, and even earthquakes. The dynamic excitations caused excessive vibration and even resonance in complex environmental conditions. Therefore, the analysis of free vibration of spherical caps becomes really meaningful.
While calculus is a powerful tool, nevertheless geometrical methods can be very effective in settings where initially it might appear that calculus has an exclusive role. For example, the focusing property of the parabola can be established with a rather simple indirect proof. It is a principle of optics that when a beam of light strikes a curved mirror at a point, the light behaves as if the mirror were flat at that point.
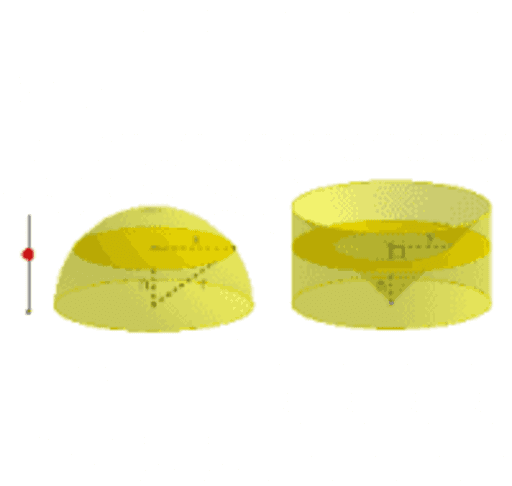
Seen on edge, a curved mirror looks like a curved line. Light in the plane of the curve striking it at a point makes equal angles with the line which is tangent to the curve at the point. The volume of a spherical sector is 23πr2h, where h is the height of the spherical cap of the spherical sector and r is the radius of the sphere. The sphere is there for comparison; the cylinder has had a cone drilled out from the top and the bottom, leaving solid material around it.
We're going to slice both the cylinder and the sphere at a height h above the center. We often get questions about deriving formulas for area and volume; usually when the question is about a sphere, the context is calculus, so we talk about integration, the usual modern method. But for students who only know geometry, "wait until you learn calculus" can be unsatisfying. Fortunately, there are a couple ways to do it using only geometrical ideas . The important thing is that they can be followed without deep knowledge. Based on the formula given earlier, H will be the height, R is the sphere radius and a is the base radius.
With the decrease of center angle, the frequency parameter of spherical cap increases, especially when the center angle is smaller than 50 degrees. To increase the accuracy of calculations, the spherical cap considered in current research is partitioned into Np shell segments along meridian direction. In addition, these sections are considered as single component in the current research.
For stepped spherical cap, the number of partition sections is related to the stepped number. Also on that page you will see an explanation of the 4/3 in the volume of the sphere. In brief, you can imagine drawing a tiny triangle on the surface of the sphere and connecting its corners to the center of the sphere.
The volume of a pyramid is 1/3 times the area of the base times the height. Thus the volume of this pyramid is 1/3 times the radius of the sphere, times the area of that little triangle. This is because the two triangles shown are similar, if slant height l is tangent to the sphere and therefore perpendicular to the radius r. The ratio \(\frac\), by the way, is the cosine of the latitude, which Randy mentioned in his question above. Usually these volume and area formulas are derived using calculus; but they were first worked out by the Greeks, notably Archimedes, using geometrical methods.




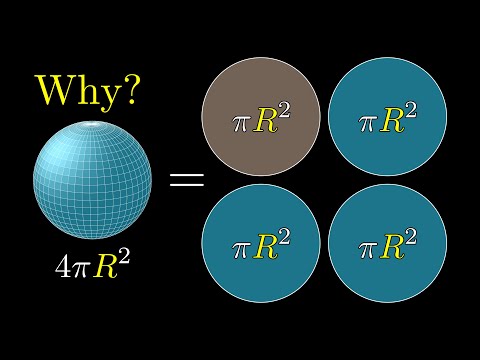



















No comments:
Post a Comment
Note: Only a member of this blog may post a comment.